Lesson 6: Present Worth of $1 Per Period
(Assessors’ Handbook 505, Column 5)
This lesson discusses the Present Worth of $1 Per Period (PW$1/P); one of six compound interest functions presented in Assessors’ Handbook Section 505 (AH 505), Capitalization Formulas and Tables. The lesson:
- Explains the function’s meaning and purpose,
- Provides the formula for the calculation of PW$1/P factors, and
- Shows practical examples of how to apply the PW$1/P factor.
PW$1/P: Meaning and Purpose
The PW$1/P is the present value of a series of future periodic payments of $1, discounted at periodic interest rate i over n periods, assuming the payments occur at the end of each period. The PW$1/P is typically used to discount a future level income stream to its present value.
Another way to conceptualize the PW$1/P is the amount that must be deposited today to fund withdrawals of $1 at the end of each of the n periods at periodic interest rate i, assuming a periodic rate i can be earned on the outstanding balance.
This compound interest function, together with the PW$1, is the basis of yield capitalization and its primary variant, discounted cash flow analysis. The PW$1/P factors are in column 5 of AH 505.
Formula for Calculating PW$1/P Factors
The formula for the calculation of the PW$1/P factors is as follows:
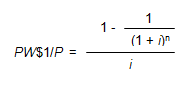
Where:
- PW$1/P = Present Worth of $1 Per Period Factor
- i = Periodic Interest Rate, often expressed as an annual percentage rate
- n = Number of Periods, often expressed in years
In order to calculate the PW$1/P factor for 4 years at an annual interest rate of 6%, use the formula below:
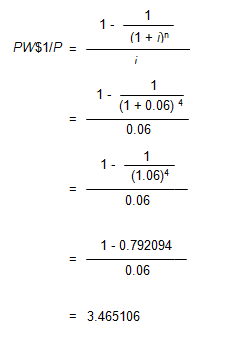
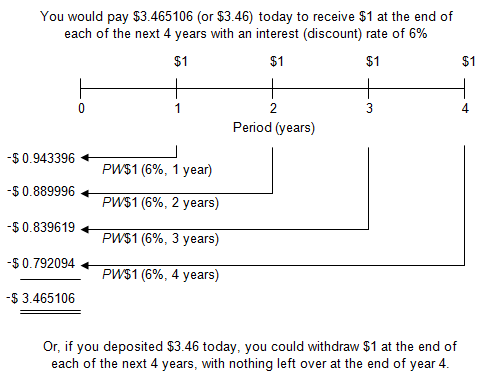
Viewed on a timeline:
On the timeline, the initial deposit of $3.465106 is shown as negative because from the point of view of a depositor it would be a cash outflow. The future values of $1 at the end of each year are shown as positive because they would be cash inflows.
To locate the PW$1/P factor, go to page 33 of AH 505, go down 4 years and across to column 5. The correct factor is 3.465106.
Practical Applications of PW$1/P
Example 1:
You’ve admired your neighbor’s vintage car for years, and he’s finally agreed to sell it to you.
He offers you the following payment alternatives:
- Pay $20,000 now, or
- Pay $6,000 at the end of each of the next 4 years with an annual interest rate of 8%
Which is the better alternative?
Solution:
- PV = PMT × PW$1/P (8%, 4 years, annual)
- PV = $6,000 × 3.312127
- PV = $19,873
Calculate the present value of the 4-year payment plan (alternative 2) using the PW$1/P factor and compare it to the immediate payment of $20,000 (alternative 1).
- Find the annual PW$1/P factor (annual compounding) for 8% at a term of 4 years. In AH 505, page 41, go down 4 years and across to column 5 to find the correct factor of 3.312127.
- The present value of $19,873 is equal to the periodic payment of $6,000 multiplied by the factor.
- You want to select the payment alternative with the lowest cost in present-value terms. Because the present value of the four payments ($19,873) is less than the immediate payment of $20,000 (no discounting of the immediate payment is required), the four-payment alternative is preferable after adjusting for the time value of money.
Example 2:
You will receive annual payments of $10,000 at the end of each year for the next 15 years with an annual interest rate of 5%. What is the present value of this stream of payments?
Solution:
- PV = PMT × PW$1/P (5%, 15 years, annual)
- PV = $10,000 × 10.379658
- PV = $103,796.58
- Find the annual PW$1/P factor (annual compounding) for 5% and 15 years. In AH 505, page 29, go down 15 years and across to column 5 to find the correct factor of 10.379658.
- The present value of $103,796.58 is equal to the periodic payment of $10,000 multiplied by the factor.
Example 3:
At the end of each year following your retirement, you want to withdraw $20,000 from your 401k retirement account.
You expect to live for 20 years after you retire. Assuming that you can earn an annual interest rate of 6%,
what balance will you need in your retirement account to fund your planned withdrawals?
Solution:
- PV = PMT × PW$1/P (6%, 20 years, annual)
- PV = $20,000 × 11.469921
- PV = $229,398
- Find the annual PW$1/P factor (annual compounding) for 6% and 20 years. In AH 505, page 33, go down 20 years and across to column 5 to find the correct factor of 11.469921.
- The present value of $229,398 is equal to the annual payment of $20,000 multiplied by the PW$1/P factor. When you retire, the balance in your account must equal the present value of the 20 years of planned future withdrawals.
Example 4:
Mr. Fortunate has won the $64 million California lottery. He will receive 20 annual payments of
$3,200,000, with the first payment to be received immediately.
Acme Investment Company is offering Mr. Fortunate $30,000,000 for the right to receive his 20 payments.
If the annual interest rate is 8% with annual compounding, should he accept the offer?
Solution:
- PV = PMT × PW$1/P (8%, 19 years, annual)
- PV = $3,200,000 × 9.603599
- PV = $30,731,517
- Total PV = $30,731,517 + $3,200,000 = $33,931,517
- Use the PW$1/P factor for 19 years to discount the future 19 payments of $3,200,000 (AH 505, page 41, column 5).
- Add the initial payment of $3,200,000 (this occurs immediately and is not discounted) to calculate the total present value of the promised payments.
- Acme is offering $30,000,000 for a stream of cash flows valued at $33,931,517 (assuming an 8% discount rate). Mr. Fortunate should decline Acme’s offer.
Example 5:
The subscription to your favorite magazine is about to expire. The magazine company offers you three renewal options:
- Pay $100 now for a four-year subscription.
- Pay $32 per year at the end of each year for four years.
- Pay $54 today and another $54 two years from today.
Assuming you want to receive the magazine for at least four more years, if the annual interest rate is 10%, which option is the best deal?
Solution:
- PV = PMT × PW$1/P (10%, 4 years, annual)
- PV = $32 × 3.169865
- PV = $101.44
- PV = FV × PW$1 (10%, 2 years, annual)
- PV = $54.00 × 0.826446
- PV = $44.63
- Total PV = $54.00 + $44.63 = $98.63
- Determine the present value of each renewal option and select the option with the lowest present value.
- The present value of option 1 is $100; payment is immediate and no discounting is required.
- The present value of option 2 is calculated using the PW$1/P factor (AH 505, page 49, column 5).
- The present value of option 3 is the initial payment of $54 (no discounting required) plus the present value of the second payment of $54 discounted for 2 years using the PW$1 factor (AH 505, page 49, column 4). Option 3 has the lowest present value and is the best deal.
