Time Value of Money - Six Functions of a Dollar
Using Assessors’ Handbook Section 505 (Capitalization Formulas and Tables)
Appraisal Training: Self-Paced Online Learning Session

Lesson 3: Present Worth of $1
(Assessors’ Handbook 505, Column 4)

This lesson discusses the Present Worth of $1 (PW$1); one of six compound interest functions presented in Assessors’ Handbook Section 505 (AH 505), Capitalization Formulas and Tables. The Lesson:

  • Explains the function’s meaning and purpose,
  • Provides the formula for the calculation of PW$1 factor,
  • Shows how to calculate the present value of multiple payments, and
  • Contains practical examples of how to apply the PW$1 factor.

PW$1: Meaning and Purpose

The PW$1 factor is the amount that must be deposited today to grow to $1 in the future, given periodic interest rate i and n periods.

The PW$1 factor is used to discount a single future amount to its present amount. The PW$1 factors are in column 4 of AH 505.

The PW$1 factor can be thought of as the opposite of the FW$1 factor; mathematically, the PW$1 and FW$1 factors are reciprocals:

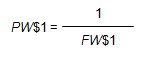
Image of an equation showing that the PW$1 factor is equal to 1 over the FW$1 factor.

Whereas the FW$1, discussed in Lesson 1, provides the future value of a single present amount, the PW$1 provides the present value of a single future amount.

The value of the PW$1 factor will always be less than $1, explicitly demonstrating that a dollar to be received in the future is worth less than a dollar today.


Formula for Calculating PW$1 Factors

The formula for the calculation of the PW$1 factors is:

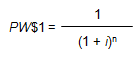
Image of an equation showing that the PW$1 factor is equal to 1 over the quantity 1 plus i raised to the power n.

Where:

  • PW$1 = Present Worth of $1 Factor
  • i = Periodic Interest Rate, often expressed as an annual percentage rate
  • n = Number of Periods, often expressed in years


In order to calculate the PW$1 factor for 4 years at an annual interest rate of 6%, use the formula below:

Image of an equation showing that the PW$1 factor is equal to 1 over the FW$1 factor, which is equal to 1 over the quantity 1 plus i raised to the power n. The value for i is 0.06 (six percent, the annual periodic rate), the value for n is 4 (four years) and the final result is 0.792094.

Viewed on a timeline:

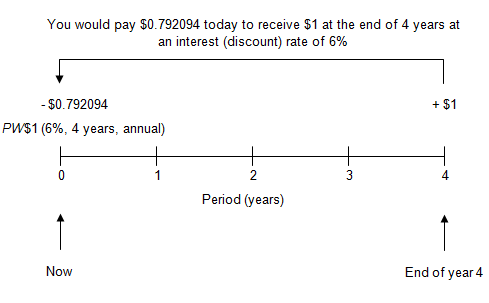
Image of a timeline showing how you would pay 0.792094 today to receive one dollar at the end of 4 years at an annual interest rate of 6 percent with annual compounding.

A depositor would be willing to give up $0.792094 today (shown as negative on the timeline) in order to receive $1 at the end of 4 years (shown as positive).

To locate the factor, go to page 33 of AH 505, go down 4 years, and then across to column 4. The correct PW$1 factor is 0.792094.


Image of a compound interest table (AH 505, page 33) highlighting the present worth of one dollar factor for 4 years with annual compounding at an annual interest rate of 6 percent. The highlighted factor is 0.792094.

Link to AH 505, page 33



Practical Applications of PW$1

Example 1:
How much must be deposited today in order to have $15,000 at the end of 10 years, assuming an annual interest rate of 7% with annual compounding?

Solution:

  • PV = FV × PW$1 (7%, 10 yrs, annual)
  • PV = $15,000 × 0.508349
  • PV = $7,625
  • Find the annual PW$1 factor (annual compounding) for 7% at a term of 10 years. In AH 505, page 37, go down 10 years and across to column 4 to find the correct factor of 0.508349.
  • The present value of $7,625 is equal to the future value of $15,000 multiplied by the factor.
Image of a compound interest table (AH 505, page 37) highlighting the present worth of one dollar factor for 10 years with annual compounding at an annual interest rate of 7 percent. The highlighted factor is 0.508349.

Link to AH 505, page 37



Example 2:
Someone promises to pay you $25,000 in 5 years. Given an annual interest rate of 6% with annual compounding, how much should you pay for this promise today?

Solution:

  • PV = FV × PW$1 (6%, 5 yrs, annual)
  • PV = $25,000 × 0.747258
  • PV = $18,681
  • Find the annual PW$1 factor (annual compounding) for 6% at a term of 5 years. In AH 505, page 33, go down 5 years and across to column 4 to find the correct factor of 0.747258.
  • The present value of $18,681 is equal to the future value of $25,000 multiplied by the factor.
Image of a compound interest table (AH 505, page 33) highlighting the present worth of one dollar factor for 5 years with annual compounding at an annual interest rate of 6 percent. The highlighted factor is 0.747258.

Link to AH 505, page 33



Example 3:
If you want to have $10,000 after 3 years, and you can invest at an annual rate of 5% compounded annually, how much should you invest today?

Solution:

  • PV = FV × PW$1 (5%, 3 yrs, annual)
  • PV = $10,000 × 0.863838
  • PV = $8,638
  • Find the annual PW$1 factor (annual compounding) for 5% at a term of 3 years. In AH 505, page 29, go down 3 years and across to column 4 to find the correct factor of 0.863838.
  • The present value of $8,638 is equal to the future value of $10,000 multiplied by the factor.
Image of a compound interest table (AH 505, page 29) highlighting the present worth of one dollar factor for 3 years with annual compounding at an annual interest rate of 5 percent. The highlighted factor is 0.863838.

Link to AH 505, page 29



Example 4:
Ten years from now, you will need to make a lump-sum payment of $500,000. Assuming annual compounding, how much should you invest today in order to cover the future payment? The annual interest rate is 10%.

Solution:

  • PV = FV × PW$1 (10%, 10 yrs, annual)
  • PV = $500,000 × .385543
  • PV = $192,772
  • Find the annual PW$1 factor (annual compounding) for 10% at a term of 10 years. In AH 505, page 49, go down 10 years and across to column 4 to find the correct factor of 0.385543.
  • The present value of $192,772 is equal to the future value of $500,000 multiplied by the factor.
Image of a compound interest table (AH 505, page 49) highlighting the present worth of one dollar factor for 10 years with annual compounding at an annual interest rate of 10 percent. The highlighted factor is 0.385543.

Link to AH 505, page 49



Example 5:
Acme Enterprises promises to pay the holders of its most recent bond issue $1,000 per bond at the end of 25 years (there are no annual or semi–annual interest payments; this is called a "zero coupon" bond). If the annual interest rate is 8.50%, assuming annual compounding, how much should each bond sell for when issued?

Solution:

  • PV = FV × PW$1 (8.50%, 25 yrs, annual)
  • PV = $1,000 × 0.130094
  • PV = $130.09
  • Find the annual PW$1 factor (annual compounding) for 8.50% at a term of 25 years. In AH 505, page 43, go down 25 years and across to column 4 to find the correct factor of 0.130094.
  • The present value of $130.09 is equal to the future value of $1,000 multiplied by the factor. The bond should sell for $130.09.
Image of a compound interest table (AH 505, page 43) highlighting the present worth of one dollar factor for 25 years with annual compounding at an annual interest rate of 8.5 percent. The highlighted factor is 0.130094.

Link to AH 505, page 43



Multiple Payments and PW$1

We have calculated the present value of single amounts or payments, using the PW$1 factors.

Many problems involve more than one payment, making it necessary to calculate the present value of multiple payments–that is, the present value of a stream of payments. Determining the present value of multiple payments is a straightforward extension of the single-payment situation.

When we calculated the present value of a single future payment, we multiplied the future payment by the appropriate PW$1 factor. This discounted the future payment to its present value.

If there is more than one future payment, multiple each payment by the appropriate PW$1 factor and add the present values. The sum of the present values is the total present value of the stream of future payments.



Practical Applications of PW$1 with Multiple Payments

Example 1:
Consider the following 3 payments:

  1. $10,000 at the end of the first year
  2. $15,000 at the end of the second year
  3. $20,000 at the end of the third year


At an annual interest rate of 5%, what is the total present value of the 3 payments?

Solution:
Calculate the present value of each payment using the PW$1 factors and add those present values. The sum is the present value of all 3 payments.

Thus:

Image showing three future payments with each payment multiplied by the appropriate PW$1 factor to arrive at the present value of the payment, then summing those present values to arrive at the total present value of the three payments. A payment of $20,000 multiplied by 0.863838, the PW$1 factor for 3 years at an annual interest rate of 5 percent, given annual compounding. The resulting present value is equal to $17,277. A payment of $15,000 multiplied by 0.907029, the PW$1 factor for 2 years at an annual interest rate 5 percent, given annual compounding. The resulting present value is equal to $13,605. A payment of $10,000 multiplied by 0.952381, the PW$1 factor for 1 year at an annual interest of 5 percent, given annual compounding. The resulting present value is equal to $9,524. Adding the three present values, the total present value of the three payments is equal to $40,406.

Image of a compound interest table (AH 505, page 29) highlighting the present worth of one dollar factor for 1, 2, and 3 years with annual compounding at an annual interest rate of 5 percent. The highlighted factors are 0.952381, 0.907029, and 0.863838.

Link to AH 505, page 29


Viewed on a timeline:

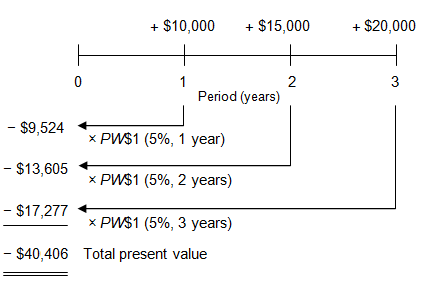
Image that depicts the calculations in the preceding table on a timeline, showing the present value for each of the three payments and the total present value of $40,406.

A person would be willing to pay $40,406 now (shown as negative on the timeline) in order to receive the three future payments of $10,000, and $15,000, and $20,000 (shown as positive).