Time Value of Money – Six Functions of a Dollar
Lesson 5 – Sinking Fund Factor
Appraisal Training: Self-Paced Online Learning Session
This lesson discusses the Sinking Fund Factor (SFF); one of six compound interest functions presented in Assessors' Handbook Section 505 (AH 505), Capitalization Formulas and Tables. The lesson:
- Explains the function's meaning and purpose
- Provides the formula for the calculation of the SFFs
- Shows practical examples of how to apply the SFF
SFF: Meaning and Purpose
The SFF is the equal periodic payment that must be made at the end of each of n periods at periodic interest rate i, such that the payments compound to $1 at the end of the last period.
The SFF is typically used to determine how much must be set aside each period in order to meet a future monetary obligation. The factors for the sinking fund are in column 3 of AH 505 (opens in a new tab).
The SFF can be thought of as the “opposite” of the FW$1/P factor; mathematically, the SFF and the FW$1/P factor are reciprocals:
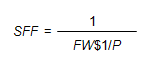
Conceptually, the FW$1/P factor provides the future amount to which periodic payments of $1 will compound, while the SFF provides the equal periodic payments that will compound to a future value of $1.
Formula for CalculatingSFF
The formula for the calculation of the SFF is
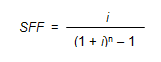
Where:
- SFF = Sinking Fund Factor
- i = Periodic Interest Rate, often expressed as an annual percentage rate
- n = Number of Periods, often expressed in years
In order to calculate the SFF for 4 years at an annual interest rate of 6%, use the formula below:
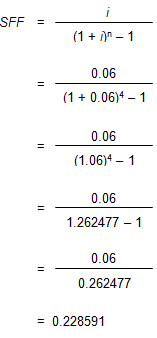
The table below shows how the sinking fund payments of 0.228591 per year compound to $1 at the end of 4 years. The payments are at the end of each year, so the beginning balance in year 1 is 0.
| Year | Beginning Balance | Annual Compounding | End of Year Payment | Ending Balance |
|---|---|---|---|---|
| 1 | 0 | n/a + | 0.228591 = | 0.228591 |
| 2 | 0.228591 | 1.06 × 0.228591 = 0.242306 + | 0.228591 = | 0.470897 |
| 3 | 0.470897 | 1.06 × 0.470897 = 0.499151 + | 0.228591 = | 0.727742 |
| 4 | 0.727742 | 1.06 × 0.727742 = 0.771407 + | 0.228591 = | 0.999998 |
| = $1 (rounding) | ||||
Viewed on a timeline:
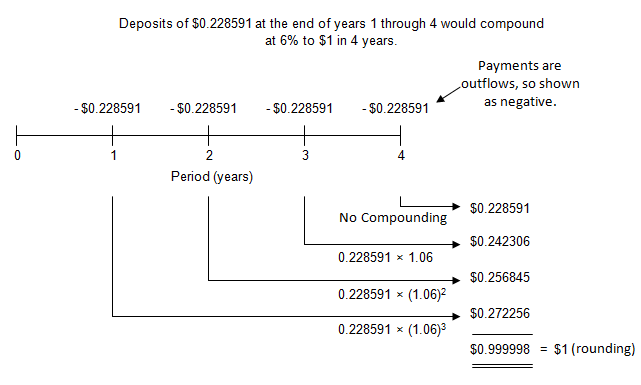
To locate the SFF, go to AH 505, page 33 (opens in a new tab), go down 4 years and across to column 3. The correct factor is 0.228591.
Practical Applications of SFF
Example 1:
A company has just issued bonds with a face value of $150 million that are due and payable in 10 years. How much should the company deposit at the end of each year in order to retire the bond issue at the end of year 10, assuming the company can earn an annual interest rate of 7% on its deposits?
Solution:
- PMT = FV × SFF (7%, 10 yrs, annual)
- PMT = $150,000,000 × 0.072378
- PMT = $10,856,700 (annual deposit required)
- Find the annual SFF (annual compounding) for 7% and a term of 10 years. In AH 505, page 37 (opens in a new tab), go down 10 years and across to column 3 to find the correct SFF of 0.072378.
- The required annual deposit, $10,856,700, is equal to the future value (the required amount at the end of year 10 multiplied by the SFF).
Example 2:
When you retire in 25 years, you would like to have $500,000 in your 401k retirement account. If you can earn an annual rate of 8%, how much should you deposit at the end of each month in order to reach your goal?
Solution:
- PMT = FV × SFF (8%, 25 yrs, monthly)
- PMT = $500,000 × 0.001051
- PMT = $525.50 (monthly deposit required)
- Find the monthly SFF (monthly compounding) for 8% and a term of 25 years. In AH 505, page 40 (opens in a new tab), go down 25 years and across to column 3 to find the correct SFF of 0.001051.
- The required monthly deposit, $525.50, is equal to the future value (amount desired upon retirement) multiplied by the SFF.
| Months | Future Worth of 1 | Future Worth of 1 per Period | Sinking Fund Factor | Present Worth of 1 | Present Worth of 1 per Period | Periodic Repayment |
|---|---|---|---|---|---|---|
| 1 | 1.006667 | 1.000000 | 1.000000 | 0.993377 | 0.993377 | 1.006667 |
| 2 | 1.013378 | 2.006667 | 0.498339 | 0.986799 | 1.980176 | 0.505006 |
| 3 | 1.020134 | 3.020044 | 0.331121 | 0.980264 | 2.960440 | 0.337788 |
| 4 | 1.026935 | 4.040178 | 0.247514 | 0.973772 | 3.934212 | 0.254181 |
| 5 | 1.033781 | 5.067113 | 0.197351 | 0.967323 | 4.901535 | 0.204018 |
| 6 | 1.040673 | 6.100893 | 0.163910 | 0.960917 | 5.862452 | 0.170577 |
| 7 | 1.047610 | 7.141566 | 0.140025 | 0.954553 | 6.817005 | 0.146692 |
| 8 | 1.054595 | 8.189176 | 0.122112 | 0.948232 | 7.765237 | 0.128779 |
| 9 | 1.061625 | 9.243771 | 0.108181 | 0.941952 | 8.707189 | 0.114848 |
| 10 | 1.068703 | 10.305396 | 0.097037 | 0.935714 | 9.642903 | 0.103703 |
| 11 | 1.075827 | 11.374099 | 0.087919 | 0.929517 | 10.572420 | 0.094586 |
Example 3:
In a balloon payment loan, only interest payments are made during the term of the loan; all of the principal is repaid at the end of the term. Suppose that you must repay a balloon loan in the amount of $1,000,000 that will be due 10 years from today. At an annual interest rate of 8%, how much should you deposit at the end of each year to fund the balloon payment?
Solution:
- PMT = FV × SFF (8%, 10 yrs, annual)
- PMT = $1,000,000 × 0.069029
- PMT = $69,029 (annual deposit required)
- Find the annual SFF (annual compounding) for 8% and a term of 10 years. In AH 505, page 41 (opens in a new tab), go down 10 years and across to column 3 to find the correct SFF of 0.069029.
- The required annual deposit, $69,029, is equal to the future value (in this case the amount of the balloon payment) multiplied by the SFF.
Example 4:
You own a small apartment building and five years from now, you expect to replace the roof at an estimated cost of $50,000. How much should you set aside at the end of each year to fund the future roof replacement, given an annual interest rate of 6%?
Solution:
- PMT = FV × SFF (6%, 5 yrs, annual)
- PMT = $50,000 × 0.177396
- PMT = $8,869.80 (annual deposit required)
- Find the annual SFF (annual compounding) for 6% and a term of 5 years. In AH 505, page 33 (opens in a new tab), go down 5 years and across to column 3 to find the correct SFF of 0.177396.
- The required annual deposit, $8,869.80, is equal to the future value (in this case the future cost of the new roof) multiplied by the SFF.
Example 5:
A borrower has a $200,000 balloon payment due in 10 years. To ensure that he can make the future payment, he plans to make equal annual deposits at the end of each year into an account that earns an annual interest rate of 4%. How much should he deposit at the end of each year?
Solution:
- PMT = FV × SFF (4%, 10 yrs, annual)
- PMT = $200,000 × 0.083291
- PMT = $16,658.20 (annual deposit required)
- Find the annual SFF (annual compounding) for 4% and a term of 10 years. In AH 505, page 25 (opens in a new tab), go down 10 years and across to column 3 to find the correct SFF of 0.083291.
- The required annual deposit, $16,658.20, is equal to the future value (in this case the amount of the balloon payment) multiplied by the SFF.
